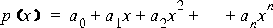
Typically, the best way to evaluate a polynomial is to use Horner's recurrence, rewriting the polynomial in the form
which requires just n additions and multiplications for an n-th degree polynomial. This example illustrates the evaluation of a small polynomial (in the square of the function argument) relating to an approximation of the sine function. It is designed specifically for use with float values.
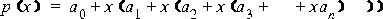
The constant float SinQ(float x) {
float_t XSq = x * x;
return -0x1.555546p-3f + XSq * (0x1.11077Ep-7f - (XSq * 0x1.9956B6p-13f));
}
0x1.555546p-3f represents the value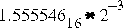 
in the float format. Although the polynomial coefficients could be expressed in decimal, it is sometimes more convenient to use hexadecimal notation. In this case, the coefficients are available in both forms in "Some Software Implementations of the Functions Sine and Cosine" by Ping Tak Peter Tang (Report ANL-90/3, Argonne National Laboratory, 1990).
[Contents]
[Previous]
[Next]
Click the icon to mail questions or corrections about this material to Taligent personnel.