sticky in the sense that it remains set until you clear it. A typical use of flags is this:
- Clear the flag of interest.
- Perform a calculation.
- Test the flag, and proceed accordingly.
To use a flag in a more global scope, you can save the state of the flag before clearing it and then either restore it or restore a modified value, depending on the calculation. This is the technique used in the implementation of library functions like Sin and Tan, in which an underflow that might arise in the evaluation of a polynomial or rational approximation is hidden from the calling code unless it is deserved because the result is tiny and inexact.
C++ exceptions
See Chapter 10 for a discussion of the connection between IEEE exception flags and C++ exception objects.
 and
and 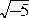 . The result is a NaN.
. The result is a NaN.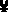 or the largest finite number, with the sign of the mathematical result. Inexact is also raised.
or the largest finite number, with the sign of the mathematical result. Inexact is also raised.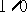 or
or 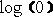 . The result is
. The result is  with appropriate sign.
with appropriate sign.