Computing a result

1. If the operation involves a NaN (for example, ), deliver one of the operand NaNs as the result. If the operation is not mathematically defined (for example, or ), raise the invalid exception flag and deliver a NaN result.
   

1. If the operation is defined as a representable limit (for example, or ) deliver the limiting value and raise any relevant flags. ( raises the divide-by-zero flag, while is zero without exception.)
   
2. If neither of the previous cases applies, the operation is mathematically defined, with a finite, real result. If that result is exactly representable in the destination format, deliver it.
   
3. Otherwise, consider the (nonzero) mathematical result to have the form , where the fraction f may be nonterminating and exponent e very large in magnitude. If the exponent is too small for the destination format, subnormalize the value-- repeatedly halving the significand and incrementing the exponent--until the exponent reaches the format's minimum. This accommodates the out-of-range exponent at the expense of precision, with a possible loss of accuracy.
   
4. The result now has the form , with e no smaller than the format's minimum. If the significand requires more than the available precision, round it by effectively adding or subtracting a small amount that replaces the mathematical result by one of the two neighboring numbers with the destination's precision that most closely bracket it from above and below. Raise the inexact flag and, if the result was subnormalized in Step 4 raise the underflow exception as well.
   The system supports four kinds of rounding:
   
   1. If rounding to nearest, choose the nearest number with the destination's precision. In case of a tie, choose the value whose least significant bit is 0.
      
   2. If rounding toward zero, chop off all bits beyond the destination's precision. That is round to the nearest neighbor toward zero.
      
   3. If rounding toward , choose the nearest more positive neighbor.
      
   4. If rounding toward , choose the nearest more negative neighbor.
      
5. The result now has the precision of the destination and the exponent is no smaller than the format's minimum. If the exponent is too large for the destination format, raise the overflow flag and proceed according to the rounding mode:
   
   1. If rounding to nearest, deliver .
      
   2. If rounding toward zero, deliver , the format's largest magnitude, with the appropriate sign.
      
   3. If rounding toward and the result is positive, or if rounding toward and the result is negative, deliver .
      
   4. Otherwise, deliver .
      

To put this process to work, consider squaring the float value to produce a float result. First, the square is a finite value so

It doesn't fit exactly into 24 significant bits, so Step 4 applies. The exponent is below so subnormalize to the form:

The braces indicate bits beyond the 24 significant bits of the float type. Proceed to Step 5. When rounding to nearest, round up to:

Raise underflow and inexact because the value was subnormalized and rounded. It can be represented as the 32-bit float value encoded as .

Closure

Alternatives

1. The exponent is below emin before rounding and the ultimate result is inexact. (This is the definition used in the recipe above. PowerPC and PA-RISC use this definition.)
   
2. The exponent is below emin after rounding and the ultimate result is inexact. (X86 uses this definition. It requires, effectively, that the tiny intermediate result by unrounded, subnormalized, and then rounded.)
   
3. The result is different due to subnormalization from what the result would be with unlimited exponent range.
   

The differences between these definitions rarely matter. Although the IEEE standards define underflow in terms of the process of detecting it, it's helpful to think of the definitions in terms of tiny results:

• If a result is exact, underflow cannot be raised.
• If a result is accurate to less than the precision of the destination, underflow must be raised. (Definition 3.)
• If the result is accurate to the precision of the destination, underflow might be raised, depending on the implementation. (Definitions 1 and 2.)

NOTE The computed value does not differ between implementations.

Sign of zero

While the real value zero is exactly representable in the floating-point number systems, its sign is an artifact outside the mathematics of real numbers. The sign of a zero result is determined as follows. First, the IEEE standards specify the sign of a zero product or quotient according to usual sign conventions for nonzero results. Similarly, the sign of the zero result of a format conversion has the sign of the source value (unless the destination is an integer format which cannot represent ). Finally, the sum of two positive zeros is ; the sum of two negative zeros is . The standards specify (arbitrarily) these ambiguous cases:

• SquareRoot( ) is .
• For any value x, the difference is , except when rounding toward , when the result is .

More generally, if f is a function of a single variable and for a floating-point value z, the sign of zero is determined by this model, which captures the sense of the IEEE specifications:

1. If for all x near z in the domain of f, then is .
   
2. If for all x near z in the domain of f, then is .
   
3. Otherwise, if , is , arbitrarily.
   
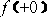4. When and the sign is not given by Step 1 or Step 2, determine the sign of and independently using one-sided limits:
   
   1. If for x just above 0, then is ; otherwise it's .
      
   2. If for x just below 0, then is ; otherwise it's .