2D and 3D GRAPHICS - List of contour curves constructor

List of contour curves constructor

This constructor creates a sweep from a list of type TCurveList and a trajectory of type TGCurve3D. TCurveList contains one or more 2-D curve geometries. When the sweep renders, the contours are blended smoothly (linearly interpolated).

To put curves into the curve list, you use the SetCurve function that wants to know where the curve goes in the list, the curve, and a u value. The u value specifies where along the sweep trajectory a given curve is to be placed.

A sweep is based on a TGSurface3D, which inhabits a parametric space defined by u and v coordinates. The contour defines the referenced TGSurface3D parametric u direction, and the trajectory defines the parametric v direction. The parametric ranges of the input curves are preserved in the created TGSurface3D.

The v parameter value can be either a parametric value that is in the same range as the trajectory or a curve arc length. The arc length is the length along the curve in the 2D or 3D coordinate system and is independent of the parameterization of the trajectory curve.

  TSweep3D(   const TCurveList& contour,
              const TGCurve3D& trajectory,
              const TGPoint3D& initialContourXDirection,
              const TGCurve& scaling = GetEmptySweepCurve,
              const TGCurve& twist = GetEmptySweepCurve,
              TGrafBundle* adoptBundle = NIL );

Contour and trajectory parameters

The contour is a 2-D curve and the trajectory is a 3-D curve. The contour and trajectory curves (like any 2-D or 3-D curve) can be closed, open, kinked, discontinuous, appear closed (with a C0 discontinuity), or have any order. Kinks are achieved by adjusting knot vectors. See Chapter 4 for information on creating curves, curve order, kinks, and discontinuity. See Chapter 14 for information on 3-D curves. Figure 174 shows an open 2D contour with a simple straight line trajectory.

Figure 175 shows four sweeps that use the same circle contour. The trajectory varies as noted for each sweep. Sweeping the contour along the different trajectories creates sweeps of various sizes and shapes as shown.

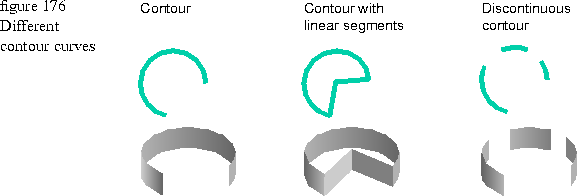
When the contour curve is discontinuous, the sweep renders in visually distinct portions. Figure 176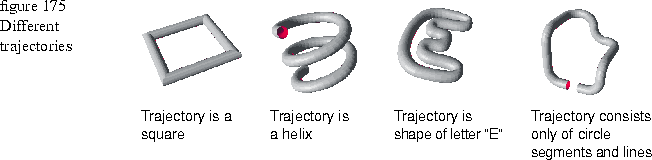 shows rendered sweeps with various contour curves.

Curve list parameter

You can use TCurveList to specify multiple contour curves to create a sweep with an unusual shape. Figure 177 shows a sweep created with three contour curves.

1  TGLoop* contour = new TGLoop( TGEllipse( TGRect( 0, 0, 200, 200 ) ) );
2  shape.ReverseDirection();
3  
4  TGLoop* contour1 = new TGLoop( TGEllipse( TGRect( 0, 0, 100, 100 ) ) );
5  shape1.ReverseDirection();
6  
7  TGLoop* contour2 = new TGLoop( TGEllipse( TGRect( 0, 0, 50, 50 ) ) );
8  shape1.ReverseDirection();
9  
10  TCurveList contourList;
11  contourList.AdoptCurve( 0, contour, 0 );
12  contourList.AdoptCurve( 1, contour2, 0.5 );
13  contourList.AdoptCurve( 2, contour1, 1 );
14  
15  TGCurve3D trajectory( TGPoint3D( 100, 0 , 100 ), 
16                          TGPoint3D( 100, 50, 100 ), 
17                          TGPoint3D( 100, 75, 100), 
18                          TGPoint3D( 100, 100, 100 ) );
19  
20  TSweep3D simpleSweep( contourList, trajectory, TGPoint3D( 1, 0, 0 ) );
21  simpleSweep.Draw( port );

Lines 1 and 2 : Create the contour. This is the same elliptical contour used in the previous code example.

Lines 4 through 8: Two more contours of different sizes.

Lines 10 through 13: Create the curve list and adopt the three contour curves. Adopting the curves requires that you specify the position in the curve list for the contour, the contour, and a parametric value to represent the location of a perpendicular plane on the trajectory in which the contour is placed. A value of 0 places the contour at the beginning of the trajectory, and a value of 1 places the contour at the end. Values between 0 and 1 place the contour on the line in proportion to the value. That is, 0.5 places the contour halfway between the beginning and the end of the trajectory.

Lines 15 through 18: Create the trajectory. This is the same piecewise linear trajectory curve used in the previous code example.

When the trajectory is a piecewise linear curve, the sweep renders as a linear constant diameter tube.
When the trajectory is a circular curve, the sweep renders as a constant curvature or constant diameter tube.
When the trajectory is a curve of arbitrary order, the sweep renders approximately and the crosssections of the sweep may not correspond exactly to the specified contour. This approximation is not visible unless extreme trajectory curves are used.

Lines 20 and 21: Create and draw the sweep.

InitialContourXDirection parameter

To begin the sweep, the contour is placed in an initial contour plane that is perpendicular to and centered around the start of the trajectory. The parameter value TGPoint3D( 1, 0 , 0 ) places the initial contour plane in the xy coordinate plane as shown inFigure 178. With this placement, the trajectory points out along the z-axis.

NOTE Currently initialContourXDirection does not work. No matter what value you supply, the contour is placed in the x-y plane as described above.

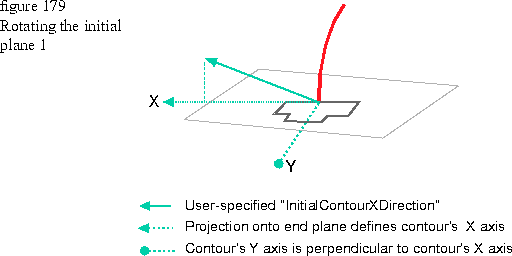
You can rotate the initial plane so that the contour does not lie in the xy plane by passing another value in the initialContourXDirection parameter. This vector is projected onto the current initial contour plane (which would be x-y, unless you previously rotated it), and becomes the x coordinate for the new initial plane with the y--axis running perpendicular to x. This concept is shown in Figure 179.

Scaling curve parameter

You can scale a contour along its trajectory with a scaling function of type TGCurve. With a scaling curve, the contour is scaled uniformly in the x and y directions. The y coordinates in the scaling curve should be 0.0 or positive. Absolute values are applied to any negative y values at run time. Figure 180 shows a scaling curve applied to two different sweeps.

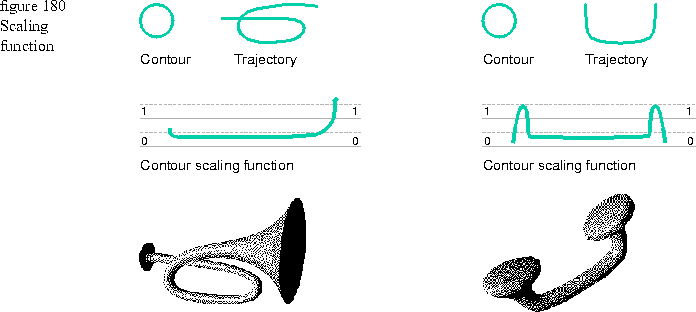
Because a scaling curve is a function, a unique y value should exist for every x value. The x-axis of the scaling curve corresponds to the distance along the trajectory. Since the trajectory distance is known to the sweep, the x coordinates of the scaling curve can have any values because those values are normalized as needed by the sweep.

The distance of the trajectory curve is the visual distance for positioning bumps in the scaling curve. If you want a scaling bump to occur about 1/3 of the distance into the trajectory, create a bump in the scaling curve about 1/3 of the distance into it.

Twist curve parameter

You can specify that a contour be twisted while it is swept along its trajectory with a twist function of type TGCurve that provides twist angle information. When you define a twisting curve, the y coordinate values are specified as degrees and should be between 0 and 360 where 0 is no turn, 180 is a half turn, and 360 is a complete turn. Values larger than 360 make the twist more than a complete turn. Figure 181 shows two sweeps and their twisting curves.

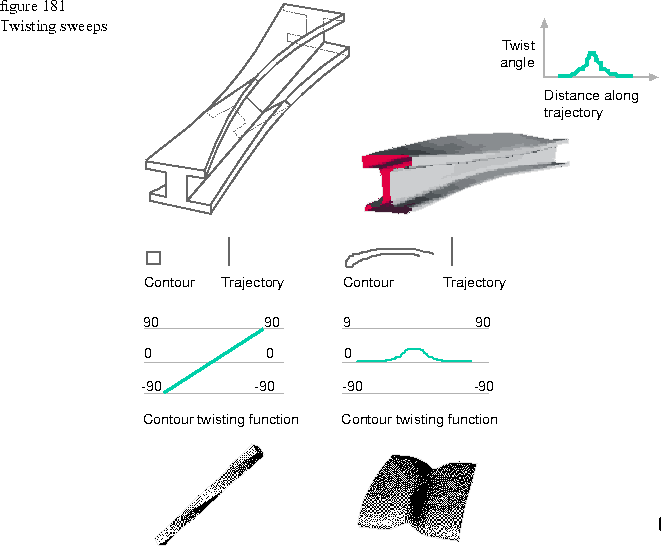
As with scaling curves, a twisting curve is a function, a unique y value should exist for every x value. The x-axis of a twisting curve corresponds to the distance along the trajectory. Since this distance is known to the sweep, the x coordinates of the twisting curve can have any values because those values are normalized as needed by the sweep.

[Contents] [Previous] [Next]

Click the icon to mail questions or corrections about this material to Taligent personnel.

Generated with WebMaker