TGrafMatrix transforms points in homogeneous space using rational points represented by the TGRPoint class described above. In homogeneous space, the third TGRPoint coordinate (fW) allows translation, rotation around an arbitrary point, scaling around an arbitrary point, perspective transformations, and shear transformations in addition to rotating and scaling around the origin through matrix multiplication. You may want to refer to a book on matrix arithmetic for more information on matrix multiplication.
NOTE  TGPoints have an implied fW of 1.0. Scaling a homogeneous matrix by a scalar does not change how it transforms a TGPoint; however, scaling a homogenous matrix by a scalar does change how it transforms a TGRPoint because a TGRPoint exists in homogeneous space.
TGPoints have an implied fW of 1.0. Scaling a homogeneous matrix by a scalar does not change how it transforms a TGPoint; however, scaling a homogenous matrix by a scalar does change how it transforms a TGRPoint because a TGRPoint exists in homogeneous space.
TGrafMatrix is not a general math package. It does not solve sets of linear equations or eigenvalue problems, and does not have arbitrary dimension. It is designed for the kinds of linear transformations (where the coordinate space is modified linearly) needed by graphics, geometries, the rendering pipeline, and GrafEdit.
Constructors
TGrafMatrix can be instantiated directly, and all of its public functions can be called directly. The default constructor creates an identity matrix. The other constructors create rotate, translate, and scale matrices. In most cases, you can avoid having to specify or know about the numbers in the matrix. One of the constructors takes a specified array of numbers; and the GetMatrix, GetElement, and SetElement functions provide access to the matrix. See the heading "Shearing transformation" on page 42 for details.
Functions
TGrafMatrix implements the full set of 2D linear affine transformations (translate, rotate, and scale) and supports concatenation (multiplying one matrix by another matrix). You can derive from TGrafMatrix to define your own transformation matrix implementation.
Table 5 lists the TGrafMatrix member functions. All functions have default implementations that you do not need to override. Refer to the online Class and Member Function descriptions for information on the TGrafMatrix functions.
|
Matrix member functions |
TGrafMatrix | ConcatWith | IsTranslate | SetToRotate |
| GetDeterminant | MakeAdjoint | SetToScale | ||
| GetElement | Normalize | SetToTranslate | ||
| GetMatrix | PreConcatWith | TransformBounds | ||
| GetRotate | PreRotateBy | TransformPoint | ||
| GetType | PreScaleBy | TransformPoints | ||
| Hash | PreTranslateBy | TransformVector | ||
| Invert | RotateBy | TranslateBy | ||
| IsAffine | ScaleBy | Transpose | ||
| IsEqual | SetElement | UntransformBounds | ||
| IsIdentity | SetToIdentity | UntransformPoint | ||
| IsRectlinear | SetToPerspectiveMap | UntransformVector |
To set up a translate, rotate, or scaling matrix, call the TranslateBy, RotateBy, and ScaleBy functions. To set up a matrix that will, for example, first scale and then rotate the graphic, call the ScaleBy and RotateBy functions in sequence. The matrix stores the cumulative transformation so you can apply one matrix to various graphics instead of scaling and rotating each graphic explicitly.
To create a sequence of arbitrary transformations rather than just translation, scaling, and rotation, use the ConcatWith function. ConcatWith concatenates two transformation matrices so that during the transformation each point passes first through one matrix and then the next. ConcatWith places the specified transformation matrix after the existing matrix.
The order by which matrices are multiplied is important because matrix multiplication is not commutative. Multiplication in one order does not necessarily give the same result as multiplication in the opposite order. For example, rotate times scale does not necessarily give the same result as scale times rotate even though the matrices are identical. You can use the PreConcatWith function to place the specified transformation matrix before the existing matrix.
SetToRotate, SetToScale, and SetToTranslate set the matrix to rotate, scale, or translate, respectively. These functions cannot be called in sequence like RotateBy, ScaleBy, and TranslateBy. If you call them in sequence, only the last call has any effect.
PreRotateBy, PreScaleBy, and PreTranslateBy premultiply this matrix by whatever values exist in the parameter list.
Perspective map transformations
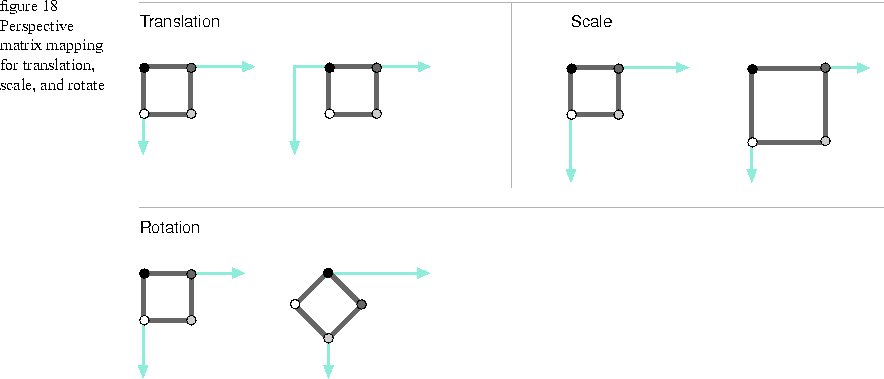
You can define a transformation matrix by specifying what a convex quadrilateral (four-sided polygon) looks like before and after the transformation. This technique is called a perspective map. You can use the TGrafMatrix:SetToPerspectiveMap function to create a perspective map to define all of the standard transformations. As shown in Figure 18, you can define a translation matrix by specifying a source polygon and a destination polygon that is the same as the source, but in a different (x,y) position; or define a scaling matrix by making the destination polygon larger or smaller than the source; or define a rotation matrix by rotating the destination polygon.
As shown in Figure 19
All matrix elements are type EMatrixIndex and can be accessed with the GetElement and SetElement functions. You can use the SetElement function to set up a shearing matrix. Once you set up the shear matrix, you can call SetToPerspective to create a perspective transformation. Figure 20 shows perspective mapping for a shear transformation.
The code below shows the SetElement function and the declaration for EMatrixIndex. Applying the matrix to a rational point (x, y, w) results in a rational point (x', y', w') using matrix multiplication:
The star is translated first and then rotated around its center.
SetToTranslate sets up a translation matrix that is overridden by SetToRotate so that only the rotation matrix is applied to the star.
PreTranslateBy and PreRotateBy translate and rotate the star, but the star is rotated around its center of origin before it is translated.
Affine and perspective transformations

Shearing transformation
A shear transformation is an affine transformation where the x coordinate of every point is changed in proportion to its y coordinate. Vectors cannot be translated; they can only be sheared. 
SetElement( EMatrixIndex index, GCoordinate& element ) const;
EMatrixIndex{
kScaleX = 0, kSheary = 1, kPerspectiveX = 2,
kShearX = 3, kScaly = 4, kPerspectivey = 5,
kTranslateX = 6, kTranslatey = 7, kHomogeneous = 8 };
2-D matrix examples
The following code fragments use the TGrafMatrix functions for translating and rotating a star. Figure 21 shows the results of the three code fragments below. In each case, the original star is framed and translated star is filled.
TranslateBy and RotateBy
aMatrix.TranslateBy( TGPoint ( 90, 20 ) );
aMatrix.RotateBy( 10, star->GetGeometricBounds().GetCenter() );
star->TransformBy( aMatrix );
star->Draw( thePort );
SetToTranslate and SetToRotate
aMatrix.SetToTranslate( TGPoint( 90, 20 ) );
aMatrix.SetToRotate( 10, star->GetGeometricBounds().GetCenter() );
star->TransformBy( aMatrix );
star->Draw( thePort );
PreTranslateBy and PreRotateBy
aMatrix.PreTranslateBy( TGPoint( 90, 20 ) );
aMatrix.PreRotateBy( 10, star->GetGeometricBounds().GetCenter() );
star->TransformBy( aMatrix );
star->Draw( thePort );
[Contents]
[Previous]
[Next]
![]() Click the icon to mail questions or corrections about this material to Taligent personnel.
Click the icon to mail questions or corrections about this material to Taligent personnel.
Generated with WebMaker