Visualizing the sweep

In the code above, the contour curve is a loop created from an ellipse in the 2-D coordinate plane. The ellipse makes the contour elliptical. If the contour curve were created from a rectangle, the contour would be rectangular instead.

The trajectory is a curve in the 3-D coordinate plane. The shape of the curve trajectory determines the path along with the contour is swept. The location of the contour in the 2-D coordinate plane is not important, only its shape and size. However, the location, shape, and length of the trajectory determine the location, shape, and length of the final sweep.

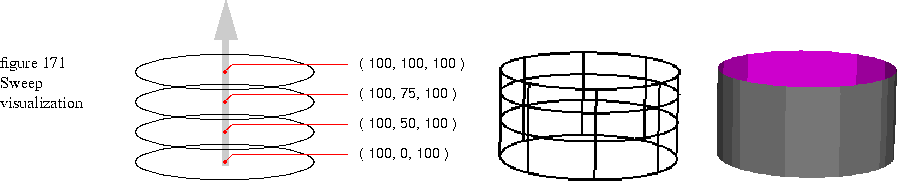
Figure 171 shows the contour and trajectory from the code example above. On the left side of the figure are the contour and trajectory with the points along the trajectory curve called out. The sweeping is a matter of centering the contour around the base of the trajectory, moving (sweeping) along the trajectory, and placing a contour at each point on the trajectory curve. In this example, the contour is swept straight up four times and covers a distance of 100 worldcoordinate units because the trajectory curve has four points that increase along the y axis from 0 to 100. The middle of the figure shows the wireframe sweep, and the right side of the figure shows the filled sweep.